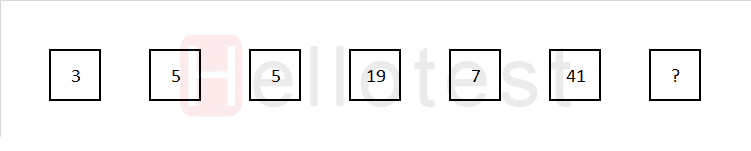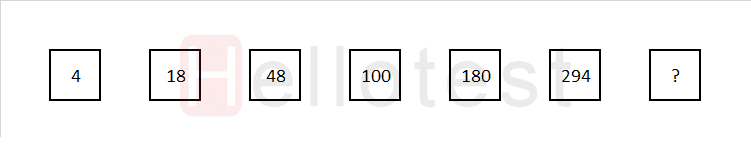Het lastige aan cijferreeksen is dat er nog een aantal variaties zijn:
- getallen overslaan;
- toenemende of afnemende veranderingen;
- reeks van berekeningen.
Daarnaast moet je ze snel en vaak zonder rekenmachine maken. Daar hebben veel mensen moeite mee. De paniek slaat toe en een slecht resultaat is het gevolg…
Geen zorgen. Cijferreeksen kun je goed oefenen. Op deze pagina leggen we enkele voorbeelden van cijferreeksen uit zodat je gratis, direct aan de slag kunt ter voorbereiding op jouw assessment.
Hoe kun je cijferreeksen oefenen?
Er zijn een aantal cijferreeksen tips en trucs om het oplossen van de reeksen te oefenen. Hieronder zullen we drie voorbeelden daarvan geven.
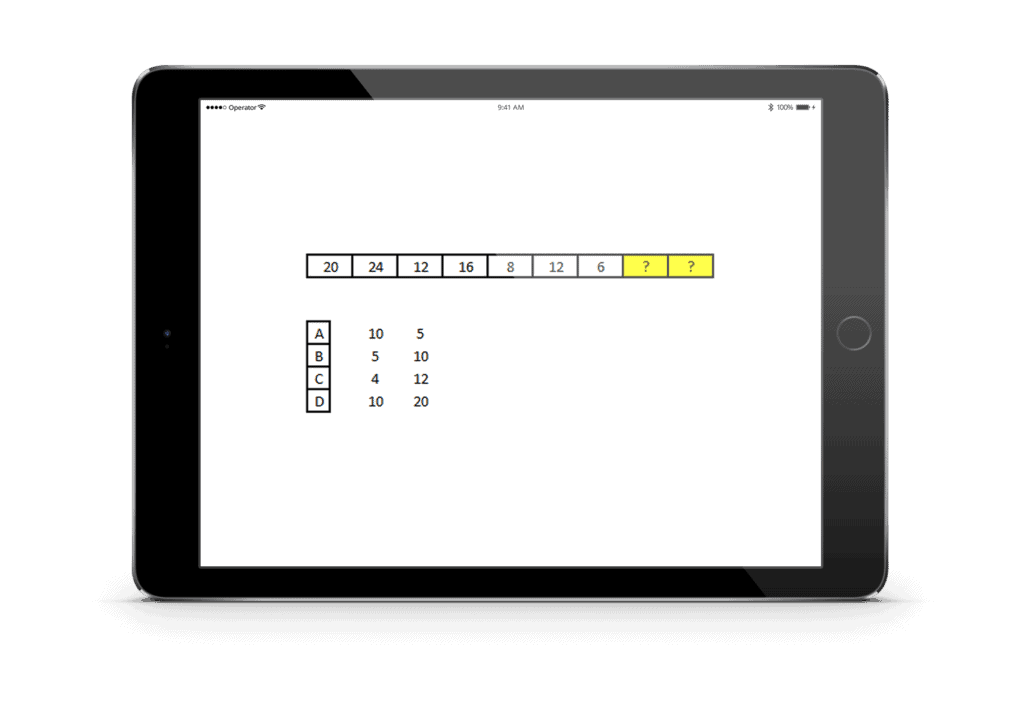
Gratis cijferreeksen oefenen met uitleg, voorbeeld 1:

Weet jij het antwoord? Dit is een bijzondere getallenreeks. Begin eerst met het uitschrijven van de verschillen tussen de getallen. Dit is eerst +7, dan +13, dan +25, dan +49 en dan +97. Hierin vallen een aantal zaken op. Namelijk dat het steeds een positieve verandering is, dat het getal steeds groter wordt en dat de verandering dichtbij de oorspronkelijke getallen uit de reeks zitten. Puur op basis van de toename is niet te voorspellen wat het volgende getal wordt.
Wat was opgevallen, is dat de verandering gerelateerd is aan het oude getal. 8*2 = 16. 15*2 = 30. 38*2 = 56, etc. Er lijkt dus een vermenigvuldiging tussen de getallen te zijn. Ook hiermee verklaar je niet de volledige getallenreeks, maar je kunt al wel een redelijke uitspraak doen over het volgende getal. Dat ligt in de buurt van 199*2 = 398.
Om exact op het goede antwoord uit te komen is nog één verdere analyse nodig. Het valt op dat de verschillen tussen de *2 en het werkelijke antwoord steeds groter worden. 8*2 -1 = 15. 15*2 -2 = 28, 28*2 -3 = 53. Hiermee komen we op de werkelijke verandering uit.
De laatste stap is 199*2 – 6 = 392.
Gratis cijferreeksen oefenen met uitleg, voorbeeld 2:
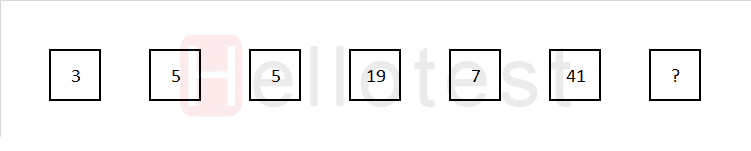
Begin met het uitschrijven van de onderliggende verschillen. De veranderingen zijn als volgt: +2, +0, +14, –12 en +34. Hierin is geen onderliggend patroon te herkennen.
Bij een dergelijke afwijkend patroon in de verandering loont het altijd om als eerste te controleren of het een dubbele getallenreeks is. Begin bij de 3, sla de eerste 5 over, sla daarna de 19 ook over. De reeks ziet er dan een stuk overzichtelijker uit: 3,5,7. Hierbij is de verandering telkens +2. Bij controle blijkt ook het volgende getal uit die reeks tot de antwoordmogelijkheden te horen waarmee de getallenreeks is opgelost. Het antwoord is 9!
Gratis cijferreeksen oefenen met uitleg, voorbeeld 3:
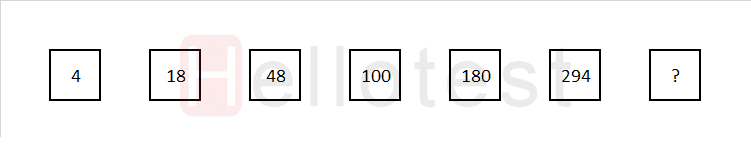
Dit is een lastige getallenreeks, ga er goed voor zitten.
De eerste stap in een cijferreeks is altijd het uitschrijven van de onderliggende verschillen. Voor bovenstaande getallenreeks is dat: +14, +30, +52, +80, +114. Hier vallen een paar zaken op, de verandering is positief, deze neemt ook toe, maar wel in veranderende snelheid.
Als je nog een laag dieper kijkt naar de toenemende verandering is die als volgt: + 16, + 22, + 28, + 34. Daarmee verwacht je dat de volgende in de reeks met 40 toeneemt. De totale toename wordt dan +154. Daarmee zou het antwoord 448 worden. Helaas, dit antwoord staat er niet tussen.
Dit is een klassieke cijferreeks waarin een zeer specifiek patroon nodig is om de cijferreeks op te lossen. Hieronder tref je de korte samenvatting aan:
2^3 – 2^2 = 8 – 4 = 4,
3^3 – 3^2 = 27 – 9 = 18,
4^3 – 4^2 = 64 – 16 = 48,
5^3 – 5^2 = 125 – 25 = 100,
6^3 – 6^2 = 216 – 36 = 180,
7^3 – 7^2 = 343 – 49 = 294.
Je ziet dat er wordt gewerkt met een complexe vergelijking. Hierbij nemen de grondgetallen telkens met +1 toe en blijven de machten gelijk. Omdat het eerste getal tot de derde macht wordt verheven wordt de uiteindelijke reeks steeds groter. Om het volgende getal in de getallenreeks te bepalen verhoog je beide grondtallen weer met één. 8^3 – 8^2 = 512 – 64 = 448.